Fostering Early Numeracy in Preschool and Kindergarten

Introduction

Over the last six decades, it has become increasingly clear that children’s everyday (informal) mathematical knowledge is an important basis for learning school (formal) mathematics.^1,2,3 Consider the long debated issue: How can students best be helped to achieve fluency with the single-digit (basic) addition facts, such as 3+4=7 and 9+5=14, and related subtraction facts, such as 7–3=4 and 14–9=5 (see, e.g., Baroody & Dowker,⁴ particularly chapters 2, 3, 6, and 7)? (Fact fluency entails generating sums and differences quickly and accurately and applying this knowledge appropriately and flexibly⁵.) Research indicates that helping children build number sense in the preschool and primary-grade years can promote fact fluency.^6,7,8,9 The aim of this entry is to summarize how the development of informal number sense before kindergarten and grades K and 1 provides a foundation for the key formal skill of addition and subtraction fact fluency in grades 2 and 3.

Key Research Questions

1. When should parents and early childhood educators begin (a) the process of promoting number sense and (b) efforts to foster fact fluency directly?
2. What are the developmental prerequisites preschoolers and kindergartners need to achieve fluency with basic sums and differences efficiently and effectively?
3. What role does language play in the development of this foundational knowledge?
4. How can parents and early childhood educators most effectively encourage number sense and fact fluency?

Recent Research Results

Question 1. The process of helping children build number sense—the foundation of fact fluency—can and should begin in the preschool years. Recent research indicates that children begin to construct number sense very early. Indeed, some toddlers as young as 18 months and nearly all 2-year-olds have begun learning the developmental prerequisites for fact fluency (e.g., see Baroody, Lai, & Mix,¹ for a review).

Successful efforts to promote fact fluency depend on ensuring a child is developmentally ready and on not rushing the child. As research indicates significant individual differences in number sense appear as early as two or three years of age and often increase with age,^1,10 there are no hard and fast rules about when formal training on fact fluency should begin. For many children though, this training, even with the easiest (n+0 and n+1) sums, may not be developmentally appropriate until late kindergarten or early first grade.¹¹ For children at risk for academic failure, work with even the easiest sums often does not make sense until first or second grade.¹²

Questions 2 and 3. Some research indicates that language, in the form of the first few number words, plays a key role in the construction of number sense (for a detailed discussion, see Baroody;³ Mix, Sandhofer, & Baroody¹³). More specifically, it can provide a basis for two foundations of early number sense—namely a concept of cardinal number (the total number of items in a collection) and the skill of verbal number recognition (VNR), usually called “subitizing,” shown at the apex of Figure 1. VNR entails reliably and efficiently recognizing the number of items in small collections and labeling them with the appropriate number word. The use of “one,” “two,” “three” in conjunction with seeing examples and non-examples of each can help 2- and 3-year-olds construct an increasingly reliable and accurate concept of the “intuitive numbers” one, two, and three—an understanding of oneness, twoness, and threeness. Consider, for example, constructing an understanding of “two”:

• By seeing various examples of pairs, such as 👟👟, 🧸🧸, ⚽️⚽️, and 🖍🖍 , all labeled “two,” young children can recognize that the appearance of the items in the collections is not important (shape and color are irrelevant to number). It can also provide them a label (“two”) for their intuitive idea of plurality (more than one item).
• Seeing non-examples of pairs, such as 👟, 🧸🧸🧸, ⚽️, and 🖍🖍🖍  labeled as “not two” or with another number word can help them define the boundaries of the concept of two.

The key instructional implications are that a basic understanding of cardinal number is not innate, nor does it unfold automatically (cf. Dehaene¹⁵).^14,16 Parents and preschool teachers are important in providing the experiences and feedback needed to construct number concepts. They should take advantage of meaningful everyday situations to label (and encourage children) to label small collections (e.g., “How many feet do you have?” “So, you need two shoes, not one.” “You may take one cookie, not two cookies.”).  Some children enter kindergarten without being able to recognize all the intuitive numbers. Such children are seriously at risk for school failure and need intensive remedial work. Kindergarten screening should check for whether children can immediately recognize collections of one to three items and be able to distinguish them from somewhat larger collections of four or five.

As Figure 1 illustrates, the co-evolution of cardinal concepts of the intuitive numbers and the skill of VNR can provide a basis for a wide variety of number, counting, and arithmetic concepts and skills—including fluency with basic addition and subtraction facts. Small-number concepts and VNR can provide a basis for meaningful verbal counting.  Recognition of the intuitive numbers can help children literally see that a collection labeled “two” has more items than a collection labeled “one” and that a collection labeled “three” has more items than a collection labeled “two.” This basic ordinal understanding of number, in turn, can help children recognize that the order of number words matters when we count (the stable order principle) and that the number word sequence (“one, two, three…”) represents increasingly larger collections. As a child becomes familiar with the counting sequence, they develop the ability to start at any point in the counting sequence and (efficiently) state the next number word in the sequence (number-after skill) instead of counting from “one.”

The ability to automatically cite the number after another number in counting sequence, can be the basis for the insight that adding “one” to a number results in a larger number and, more specifically, the number-after rule for n+1/1+n facts. When adding “one”, the sum is the number after the other number in the counting sequence (e.g., the sum of 7+1 is the number after “seven” when we count or “eight”).

Figure 1. Learning Trajectory of Some Key Number, Counting, & Arithmetic Concepts and Skills

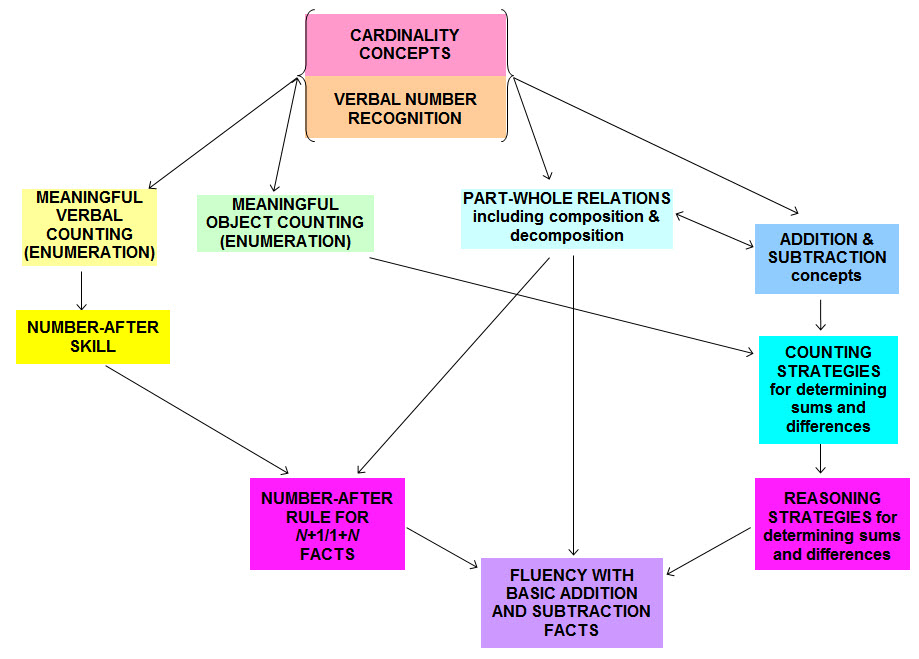
This reasoning strategy can enable children to efficiently deduce the sum of any such combination for which they know the counting sequence, even those not previously practiced including large multi-digit facts such as 28+1, 128+1, or 1,000,128+1. In time, this reasoning strategy becomes automatic—can be applied efficiently, without deliberation (i.e., becomes a component in the retrieval network). In other words, it becomes the basis for fact fluency with the n+1/1+n combinations.

VNR, and the cardinal concept of number it embodies, can be a basis for meaningful object counting.¹⁷ Children who can subitize collections up to “four” are more likely to benefit from adult efforts to model and teach object counting than those who cannot. When modeling involves counting and then labeling a collection within a child’s subitizing range, they are also more likely to recognize the purpose of object counting (as another way of determining a collection’s total) and the rationale for object-counting procedures (e.g., the reason why others emphasize or repeat the last number word used in the counting process is because it represents the collection’s total).¹⁸ Meaningful object counting is necessary for the invention of counting strategies (with objects or number words) to determine sums and differences. As these strategies become efficient, attention is freed to discover patterns and relations; these mathematical regularities, in turn, can serve as the basis for reasoning strategies (i.e., using known facts and relations to deduce the answer of an unknown combination). As these reasoning strategies become automatic, they can serve as one of the retrieval strategies for efficiently producing answers from a memory or retrieval network.

VNR can enable a child to see one & one as two, one & one & one as three, or two & one as three and the reverse (e.g., three as one & one & one or as two & one).  The child thus constructs an understanding of composition and decomposition (a whole can be built up from, or broken down into, individual parts, often in different ways). Repeatedly seeing the composition and decomposition of two and three can lead to fact fluency with the simplest addition and subtraction facts (e.g., “one and one is two,” “two and one is three,” and “two take away one is one”). Repeatedly decomposing four and five with feedback (e.g., labeling a collection of four as “two and two”, and hearing another person confirm, “Yes, two and two makes four”) can lead to fact fluency with the simplest sums to five and is one way of discovering the number-after rule for n+1/1+n combinations (discussed earlier).

The concept of cardinality, VNR, and the concepts of composition and decomposition can together provide the basis for constructing a basic concept of addition and subtraction. For example, by adding an item to a collection of two items, a child can literally see that the original collection has been transformed into a larger collection of three. These competencies can also provide a basis for constructing a relatively concrete, and even a relatively abstract, understanding of the following arithmetic concepts¹⁹:

• Concept of subtractive negation. For example, when children recognize that if you have two blocks and take away two blocks this leaves none, they may induce the pattern that any number take away itself leaves nothing.
• Concept of additive and subtractive identity. For example, when children recognize that two blocks take away none leaves two blocks, they may induce the regularity that if none is taken from any number, the number will remain unchanged. The concepts of subtractive negation and subtractive identity can provide a basis for fact fluency with the n – n = 0 and n – 0 = n families of subtraction facts, respectively.

A weak number sense, then, can interfere with achieving fact fluency and other aspects of mathematical achievement. For example, Mazzocco and Thompson²⁰ found that preschoolers’ performance on the following four items of the Test of Early Mathematics Ability—Second Edition (TEMA-2) was predictive of which children would have mathematical difficulties in second and third grade: meaningful object counting (recognizing that the last number word used in the counting process indicates the total), cardinality, comparing of one-digit numbers (e.g., Which is more five or four?), mentally adding one-digit numbers, and reading one-digit one numerals. Note that verbal number recognition of the intuitive numbers is a foundation for the first three skills and meaningful learning of the fourth.

Question 4. The basis for helping students build both number sense in general and fact fluency in particular is creating opportunities for them to discover patterns and relations. For example, a child who has learned the “doubles,” such as 5+5=10 and 6+6=12, in a meaningful manner (e.g., the child recognizes that the sums of this family are all even or count-by-two numbers) can use this knowledge to reason out the sums of unknown doubles-plus-one facts, such as 5+6 or 7+6.

To be developmentally appropriate, such learning opportunities should be purposeful, meaningful, and inquiry based.²¹

• Instruction should be purposeful and engaging to children. This can be achieved by embedding instruction in structured play (e.g., playing a game that involves throwing a die can help children learn to recognize regular patterns of one to six). Music and art lessons can serve as natural vehicles for thinking about patterns, numbers, and shapes (e.g., keeping a beat of two or three; drawing groups of balloons). Parents and teachers can take advantage of numerous everyday situations (e.g., “How many feet do you have? …So, how many socks should you get from your sock drawer?”). Children’s questions can be an important source of purposeful instruction.
• Instruction should be meaningful to children, building gradually on (and being connected to) what they know. A meaningful goal for adults working with 2-year-olds is to have children recognize two. Pushing them too fast to recognize larger numbers such as four can be overwhelming, causing them to melt down (become inattentive or aggressive, guess wildly, or otherwise disengage from the activity).
• Instruction should be inquiry based, or thought provoking, to the extent possible. Instead of simply feeding children information, parents and teachers should give children an opportunity to think about a problem or task, make conjectures (educated guesses), devise their own strategies or deduce their own answer.

The various points above are illustrated by the case of Alice²² and Lukas.²³

• The case of Alice. The 2.5-year-old had for several months been able to recognize one, two, or three things. So, her parents wanted to expand her number range to four, which was now just outside her range of competence. Instead of simply labeling collections of four for her, they asked her about collections of four. Alice often responded by decomposing the unrecognizable collections into two familiar collections of two. Her parents then built on her response by saying, “Two and two is four.” At 30 months of age, shown a picture of four puppies, Alice put two fingers of her left hand on two dogs and said, “Two.” While maintaining this posture, she placed two fingers of her right hand on the other two puppies and said, “Two.” She then used the known relation “2 and 2 makes 4” (learned from her parents) to specify the cardinal value of the collection.
• The case of Lukas. In the context of a computer-based math game, Lukas was presented 6+6. He determined the sum by counting. Shortly afterward, he was presented 7+7. He smiled and answered quickly, “Thirteen.” When the computer feedback indicated the sum was 14, he seemed puzzled. A couple of items later, he was presented 8+8 and noted, “I was going to say 15, because 7+7 was 14. But before 6+6 was 12, I thought for sure that 7+7 would be 13 but it was 14. So, I’m going to say 8+8 is 16.”

The Case of Fostering Fluency with Subtraction Facts: The Long View

To illustrate the implications of the recent research previously discussed, consider the case of promoting fluency with the more challenging facts basic subtraction facts such as 8–5 and 15–7. Mathematics educators, textbook publishers, and educational policy makers often routinely recommend helping children learn such facts by helping them learn a subtraction-as-addition reasoning strategy (e.g., for 8–5, think: “What added to five makes eight?”).^24,25 The short view, which is too commonly practiced, is to impose (e.g., demonstrate or illustrate) the reasoning strategy and perhaps attempt a brief explanation of it. Limited practice with the strategy is then used to promote its automaticity. A serious limitation of the short view is that many children do not understand the strategy. This can result in memorizing it correctly but not applying when appropriate or forgetting it altogether, memorizing it by rote incorrectly, or not making any effort to memorize it at all.

The long view is that fluency with the subtraction-as-addition strategy cannot be promoted in days, weeks, months, or even a year. Children’s informal and formal experiences often leads them to believe that addition and subtraction are unrelated operations and that knowledge of one cannot help with thinking about the other. The key to achieving fluency with basic difference meaningfully and effectively is (a) discover how the operations of addition and subtraction are related, (b) achieve fluency with related sums, and (c) then practice using this integrated knowledge until it becomes automatic.^26,27 As the learning trajectory depicted in Figure 2 indicates, the process of building the number sense for such a path to fluency is a gradual and begins in the preschool years.

• As previously noted, VNR provides a basis for an informal understanding of addition as a means for making a collection larger and subtraction as making a collection smaller (Concept 1 in Figure 2). These informal concepts of addition and subtraction provide a basis for understanding and (informally) solving word problems and symbolic expressions such as 7–4 and equations such as 7–4 = ?
• VNR can also provide a basis for experiences with empirical inversion—situations where a few items are added to (removed from) a small collection, the same number of items are then removed (or added), and the collection is restored to its original number). Such experiences can help children discover the undoing concept: addition and subtraction are related because adding and then subtracting the same number of items or vice versa leaves the original number of items (Concept 2 in Figure 4). This informal undoing concept provides a basis for understanding formal (written) representations of the concept, such as 7+4–4 = 7 and recognizing the shared-numbers concept (equations such as 7+4 = 11 and 11-4 = 7 are related and share the same three numbers; Concept 4 in Figure 2).
• VNR can also help children construct informal composition and decomposition concepts (Concept 3 in Figure 2), which are the basis for a more formal part-whole view of addition and subtraction (Concept 4 in Figure 2). It permits children to imagine that two (small and nearby) collections (“parts”) can be thought as a single, larger collection (“whole”) or that a larger whole collection can be thought of two smaller groups (parts). For example, seeing a dice roll of •• and •• as “two” and another “two” and also seeing (or hearing an older player) label it as “four” can help a child see that two (smaller) collections of “two” can be re-imagined as parts of the (larger) collection or whole of “four” and the whole “four” can be re-imagined as the smaller parts of “two” and “two.” Moreover, also seeing a dice roll of • and ••• as "one" and a “three" and as “four” can lead to the insight that different combinations of smaller collections or parts can make the same larger number or whole or that a whole can be separated into smaller groups or parts. Once children learn to read written numbers, children can relate their informal knowledge of composition and decomposition to written expressions such as 2+2 or 1+3 and written equations such as 2+2 = 4 or 1+3 = 4 and construct the following formal concepts:
  • Specifically, basic informal concepts of composition and decomposition and part-whole ideas can provide a basis for a formal interpretation of an addition equation such as 1+3 = 4 as the parts 1 and 3 compose the larger whole 4 (as opposed to informal view a collection of one is made larger by adding three more) and 4–3 = 1 as the larger whole 4 is composed of the known part 3 and the unknown part 1 (Concept 5 in Figure 2: formal part-whole knowledge of addition and subtraction). Viewing addition and subtraction in terms of such a part-whole meaning supports the conclusion that subtracting a part from a whole leaves a part that is smaller than the whole
  • Even before constructing a formal part-whole view of addition and subtraction (Concept 5 in Figure 2), elements of informal composition and decomposition can help children construct a formal shared-numbers concept:  An understanding that the written expressions 1+6, 2+5, 3+4, 4+3, 5+2, and 6+1 all have the same sum (whole) 7 and, conversely, the number (whole) 7 can also be represented by the expressions 1+6, 2+5, 3+4, 4+3, 5+2, and 6+1. For both reasons, 1+6, 2+5, 3+4, 4+3, 5+2, and 6+1 form a “family of sums.” Importantly, this can lead to recognizing families of sums are related to families of differences and that all family members consist of the three same three numbers (Concept 4 in Figure 2: the shared-numbers concept).

As the learning trajectory depicted in Figure 2 suggests, deepening an understanding the operation of subtraction and its relation to addition, which strengthen the foundation for achieving fluency with basic differences, can be realized in kindergarten and grade 1.

• The shared-number concept can be underscored by using—as is done in Everyday Mathematics program—“fact triangles” (see, e.g., Figure 3 or—for a detailed discussion—Baroody²⁶). 
• Formal part-whole knowledge of addition and subtraction can be fostered, in part, by explicitly labeling the elements of a fact triangle as a “whole” or a “part” (e.g., using an asterisk to note the “whole” or labeling 3+4 = 7 as “the part three and the part four make the total seven”). Fact rectangles can provide a relatively concrete representation of part-whole relations (see, e.g., Figure 4 or—for a detailed discussion—Baroody²⁶). Solving part-whole word problems (see, e.g., Figure 5) can be helpful also.
• Promoting both the shared-number concept and formal part-whole knowledge in an integrated manner can foster the shared parts and whole concept: An addition-subtraction family of facts share the same whole and parts. The understanding provides a basis for recognizing the complement principle discussed in the next paragraph.

As the learning trajectory depicted in Figure 2 suggests, the final key elements for constructing subtraction-as-addition reasoning strategy and automatizing this strategy can now be achieved grade 2 or 3. 

• Fluency with basic sums to 18 can greatly facilitate using the subtraction-as-addition strategy to reason out consciously and then automatically subtraction facts.
• Discovering another key relation between addition and subtraction—the complement principle (e.g., if the parts 5 and 3 make the whole 8, then the whole 8 minus the part 3 leaves the part 5) —can provide a basis for understanding why the addition-as-subtraction strategy works and better enable children to internalize it.
• Practice using the subtraction-as-addition strategy can serve to automatize it and achieve fluency with differences to 18.

Figure 2: Learning Trajectory for the Meaningful Development of the Subtraction-as-Addition Reasoning (Subtraction) Strategy

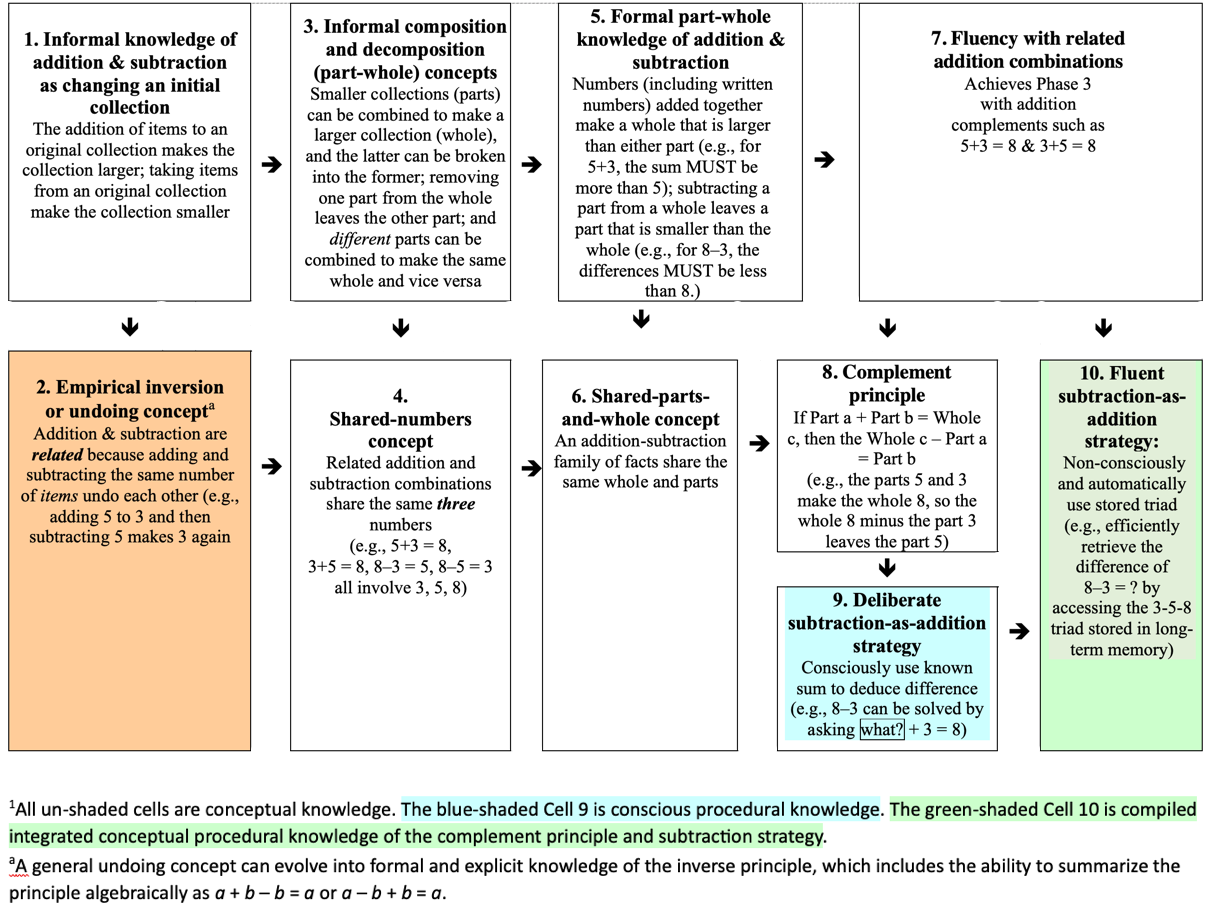
Figure 3. Fact Family Triangle

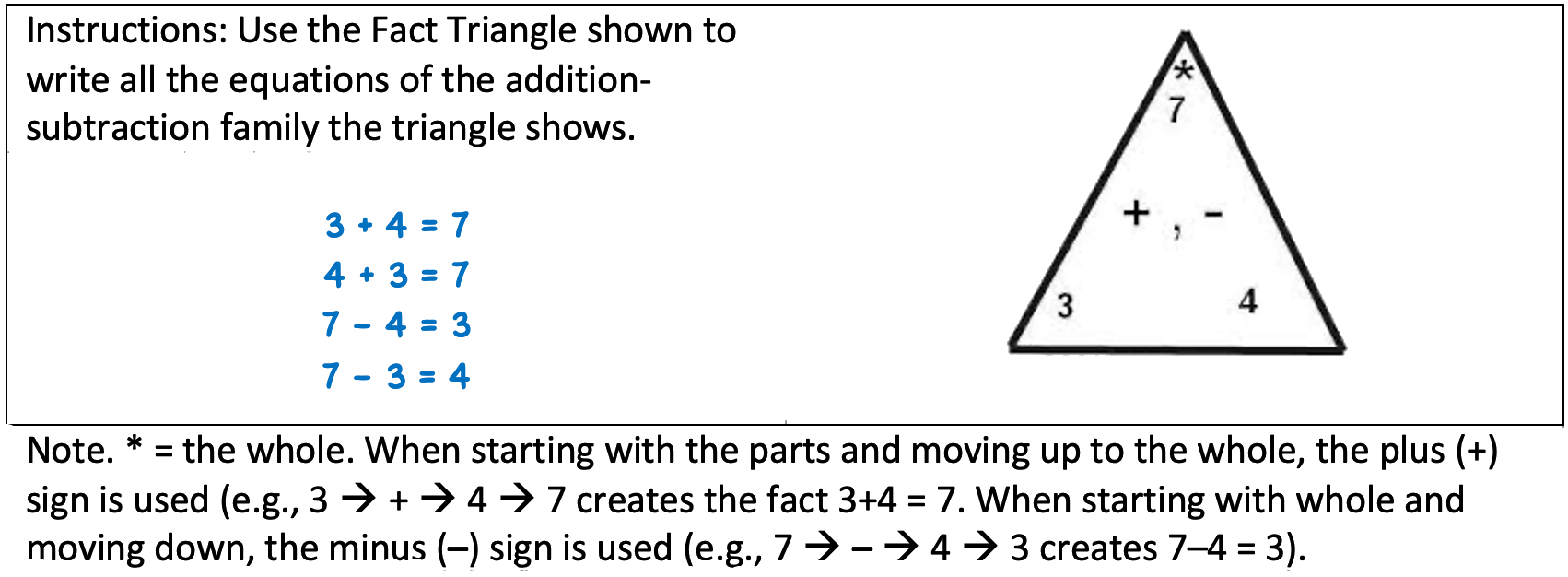
Figure 4. Fact Rectangles

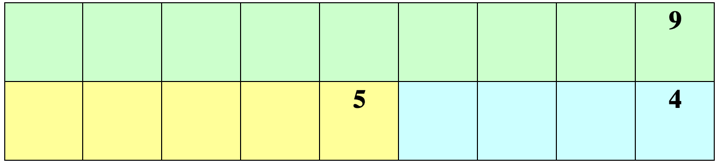
Figure 5. Example of Part-Part-Whole Word Problem

Word Problem
Aza had seven toy trucks. Four were blue and the rest were red. How many red trucks did Aza have?

Part-Part-Whole Picture

Equation:  4 + ? = 7 or 7 – 4 = ?

Answer:    3

Future Directions

Much still needs to be learned about preschoolers’ mathematical development. Does VNR ability at two years of age predict readiness for kindergarten or mathematical achievement in school? If so, can intervention that focuses on examples and non-examples enable children at risk for academic failure to catch up with their peers? What other concepts or skills at two or three years of age might be predictive of readiness for kindergarten or mathematical achievement in school? How effective are the early childhood mathematics programs currently being developed?

Conclusions

Contrary to the beliefs of some early childhood educators, mathematics instruction for children as young as two years of age does make sense.^28,22,30,31 As Figure 1 makes clear, this instruction should start with helping children construct a cardinal concept of the intuitive numbers and the skill of recognizing and labeling sets of one to three items with an appropriate number word. As Figure 1 further illustrates, these aspects of number knowledge are key to later numeracy and often lacking among children with mathematical disabilities.³² For example, although memorizing the basic subtraction facts is often challenging, even difficult, or unobtainable for many children, it need not be if instruction helps children build number sense by discovering key arithmetic regularities at both the preschool and primary levels. Early instruction does not mean imposing knowledge on preschoolers, drilling them with flashcards, or otherwise having them memorize by rote arithmetic facts. Fostering number sense and fact fluency both should focus on helping children discover patterns and relations and encouraging their invention of reasoning strategies.

The research described was supported, in part, by a grant from the National Science Foundation (BCS-0111829), the Spencer Foundation (Major Grant 200400033), the National Institutes of Health (1 R01 HD051538-01), and the Institute of Education Science (R305K050082 and R305A080479). Update of this report was supported by grants from the National Science Foundation (1621470 and 2201939.) The opinions expressed in the present manuscript are solely those of the author and do not necessarily reflect the position, policy, or endorsement of the aforenamed institutions.

References

1. Baroody AJ, Lai ML, Mix KS. The development of number and operation sense in early childhood. In: Saracho O, Spodek B, eds. Handbook of research on the education of young children. Mahwah, NJ: Erlbaum; 2006: 187-221.
2. Clements D, Sarama J, DiBiase AM, eds. Engaging young children in mathematics: Standards for early childhood mathematics education. Mahwah, NJ: Lawrence Erlbaum Associates; 2004: 149-172.
3. Ginsburg HP, Klein A, Starkey P. The development of children’s mathematical knowledge: Connecting research with practice. In: Sigel IE, Renninger KA, eds. Child psychology in practice. 5th Ed. New York, NY: Wiley & Sons; 1998; 401-476. Handbook of child psychology, vol 4.
4. Baroody AJ, Dowker A. The development of arithmetic concepts and skills: Constructing adaptive expertise. In: Schoenfeld A, ed. Studies in mathematics thinking and learning series. Mahwah, NJ: Lawrence Erlbaum Associates; 2003.
5. Kilpatrick J, Swafford J, Findell B, eds. Adding it up: Helping children learn mathematics. Washington, DC: National Academy Press; 2001.
6. Baroody AJ, Bajwa NP, Eiland M. Why can’t Johnny remember the basic facts? Developmental Disabilities Research Reviews 2009;15(1):69-79. (Special issue on “Pathways to Mathematical Learning Disabilities,” guest edited by M. Mazzocco.) doi:10.1002/ddrr.45
7. Baroody AJ, Purpura DJ. Early number and operations: Whole numbers. In: Cai J, ed. Compendium for research in mathematics education. Reston, VA: National Council of Teachers of Mathematics; 2017:308-354.
8. Gersten R, Chard, D. Number sense: Rethinking arithmetic instruction for students with mathematical disabilities. The Journal of Special Education 1999;33(1):18–28.
9. Jordan NC. The need for number sense. Educational Leadership. 2007;65(2):63-66.
10. Dowker AD. Individual differences in arithmetic: Implications for psychology, neuroscience and education. Hove, England: Psychology Press; 2005.
11. Baroody AJ. The development of kindergartners' mental-addition strategies. Learning and Individual Differences 1992;4:215-235.
12. Baroody AJ, Eiland M, Thompson B. Fostering at-risk preschoolers' number sense. Early Education and Development 2009;20:80-120.
13. Mix KS, Sandhofer CM, Baroody AJ. Number words and number concepts: The interplay of verbal and nonverbal processes in early quantitative development. In: Kail R, ed. Advances in child development and behavior, vol 33. New York, NY: Academic Press; 2005: 305-346.
14. Baroody AJ, Li X, Lai ML. Toddlers’ spontaneous attention to number. Mathematics Thinking and Learning 2008;10:1-31.
15. Dehaene S. The number sense. New York, NY: Oxford University Press; 1997.
16. Wynn K. Numerical competence in infants. In: Donlan C, ed. Development of mathematical skills. Hove, England: Psychology Press; 1998:1-25.
17. Benoit L, Lehalle H, Jouen F. Do young children acquire number words through subitizing or counting? Cognitive Development 2004;19:291-307.
18. Paliwal V, Baroody AJ. Cardinality principle understanding: The role of focusing on the subitizing ability. ZDM Mathematics Education 2020;52(4):649-661. doi:10.1007/s11858-020-01150-0
19. Baroody AJ, Lai ML, Li X, Baroody AE. Preschoolers’ understanding of subtraction-related principles. Mathematics Thinking and Learning 2009;11:41-60.
20. Mazzocco M, Thompson R. Kindergarten predictors of math learning disability. Learning Disabilities Research & Practice 2005;20:142-155.
21. Baroody AJ, Coslick RT. Fostering children's mathematical power: An investigative approach to K-8 mathematics instruction. Mahwah, NJ: Erlbaum; 1998.
22. Baroody AJ, Rosu L. Adaptive expertise with basic addition and subtraction combinations: The number sense view. In: Baroody AJ, Torbeyns T. chairs. Developing Adaptive 
    Expertise in Elementary School Arithmetic. Symposium conducted at: The annual meeting of the American Educational Research Association. April, 2006. San Francisco, CA.
23. Baroody AJ. Fostering early number sense. Keynote address at: The Banff International Conference on Behavioural Science. March, 2008. Banff, Alberta.
24. National Council of Teachers of Mathematics. Curriculum focal points for prekindergarten through grade 8 mathematics. Reston, VA: Author; 2006.
25. National Governors Association Center for Best Practices and Council of Chief State School Officers. Common Core State Standards: Preparing America’s students for college and career.
26. Baroody AJ. Curricular approaches to introducing subtraction and fostering fluency with basic differences in grade 1. In: Bracho R, ed. The development of number sense: From theory to practice. Monograph of the Journal of Pensamiento Numérico y Algebraico [Numerical and Algebraic Thought] 2016;10(3):161–191. University of Granada.
27. Baroody A J, Purpura D J, Eiland MD, Reid EE, Paliwal V. Does fostering reasoning strategies for relatively difficult basic combinations promote transfer? Journal of Educational Psychology 2016;108: 576–591. doi: 10.1037/edu0000067
28. Baroody AJ, Li X. Mathematics instruction that makes sense for 2- to 5-year-olds. In: Essa EA, Burnham MM, eds. Development and education: Research reviews from young children. New York: The National Association for the Education of Young Children; 2009: 119-135.
29. Bredekamp S, Copple C. Developmentally appropriate practice in early childhood programs. Washington, DC:  National Association for the Education of Young Children; 1997.
30. Copley J, ed.  Mathematics in the early years, birth to five. Reston, VA: National Council of Teachers of Mathematics; 1999.
31. Copley J, ed. The young child and mathematics. Washington, DC: National Association for the Education of Young Children; 2000.
32. Landerl K, Bevan A, Butterworth B. Developmental dyscalculia and basic numerical capacities: A study of 8–9-year-old students. Cognition 2004;93:99-125.